In sports betting, the hook is paying additional vig to get half a point. In laymen terms, it’s risking a larger amount of money to win the same amount of money to move the spread .5 points in the bettors favor. For example, if wagering on a 3.5 point favorite and buying the hook the spread will now be 3 points. But to gain this advantage the bettor will have to risk $120 to win $100 (120/100) instead of $110 to win $100 (110/100). Thus, the price of the hook was $10 but obtained the bettor a more favorable spread.
A good rule of thumb is that any change to a bet offered will be to the advantage of the party who who takes the bet. This rule applies not just to sports betting but to casino table games generally. An example is the insurance bet in blackjack which reduces variance of outcome but is expected positive value for the dealer.
However, it is possible to determine the value of the hook using a sufficiently large data set of college football games [1]. Using the population of games, the likelihood of the hook influencing the bet’s outcome can be calculated which can then be used to determine the value of the hook.
A prior post covered college football spreads and explained the spread error [2] and looked at it as an average and standard deviation. For the purposes of this analysis, it’s helpful to look at a histogram of the spread errors. This visual shows that more than half the spread errors are worth more than a touchdown but the largest histogram bin is zero to the first point so we know many games are close and a point can matter.

To determine the exact value of the hook, each game must be simulated with the an adjustment to the spread. First for the favorite. Below are 20 data points which recalculate the outcome with the spread changed by half-point increments from .5 to 10 points and the percentage of games that change. The visual is a clear linear line from 0% at zero points to 25% of games at 10 points.

Looking at the incremental change, we see the value of the incremental half-point is within a narrow 1%-1.7% range. This implies that while the first half-point is slightly more valuable (1.7%) than the average over the first 20 half-points (1.2%) the actual number of games that are impacted by the hook is very small. We can safely assume that the hook will impact less than 2% of bets.

Popular advise is to buy the the hook for single score spreads (i.e., -3.5, -7.5) where a half-point is the difference between a single score such as a field goal or touchdown. To understand single score spreads and single score games, the following bar chart is game margins with single score games in red [3].

Clearly, we can see that these single score game margins are more common than other type of game margins. Games are 2.5 to 3.5 times more likely to end in a 3 or 7 point margin than 2, 4, 6 or 8 points.
The following visual shows that by odds, games with a 2.5-3.5 and 6.5-7.5 point spread are indeed more likely to be impacted [4] by a half-point adjustment with those spreads highlighted in red.
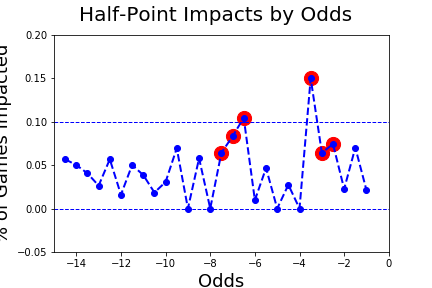
In fact, games with a spread of 2.5-3.5 and 6.5-7.5 are impacted by a half-point in 9% of bets while the average for the entire population is 4.7% of games. And this statistic answers the original question as to the value of the hook. For spreads of 2.5-3.5 and 6.5-7.5, the value of the hook is roughly 4.5% of the bet [5] while for all other games the hook is worth roughly 1.8% of the bet [6].
[1] The data set referenced is a 4,718 college football games from 2014-2018 with a spread and outcome.
[2] The spread error is defined as the difference between the spread and the actual game outcome. For example, if the spread is -7 points and the favorite wins by 8, the error would be 1. Alternatively, if the spread is -7 and the favorite loses by 1 the error would be 8.
[3] Single score game is a game result with the winning team margin of victory equal to the two most common scoring events in football, a touchdown plus extra point (7 points) and a field goal (3).
[4] Impacted is defined as a bet outcome which would be changed by a half-point adjustment. Earlier it was noted that a half-point change would cause the favorite to cover in less than 2% of games. However, impacted also includes games where the underdog would now cover as well as games where neither team would cover but a push would now occur. This explains the differential between the ~2% and ~4.5% between the two metrics.
[5] This calculation is approximately half the value of the likelihood of the half-point impacting the game. Importantly you must assume that you have no special insight into the outcome and thus there is a 50% chance your bet will be wrong and the half-point will be irrelevant.
[6] This is lower than the general average as you must remove the higher likelihood odds of 2.5-3.5 and 6.5-7.5 then recalculate the percentage of games impacted which becomes 3.6% compared to 4.7%.